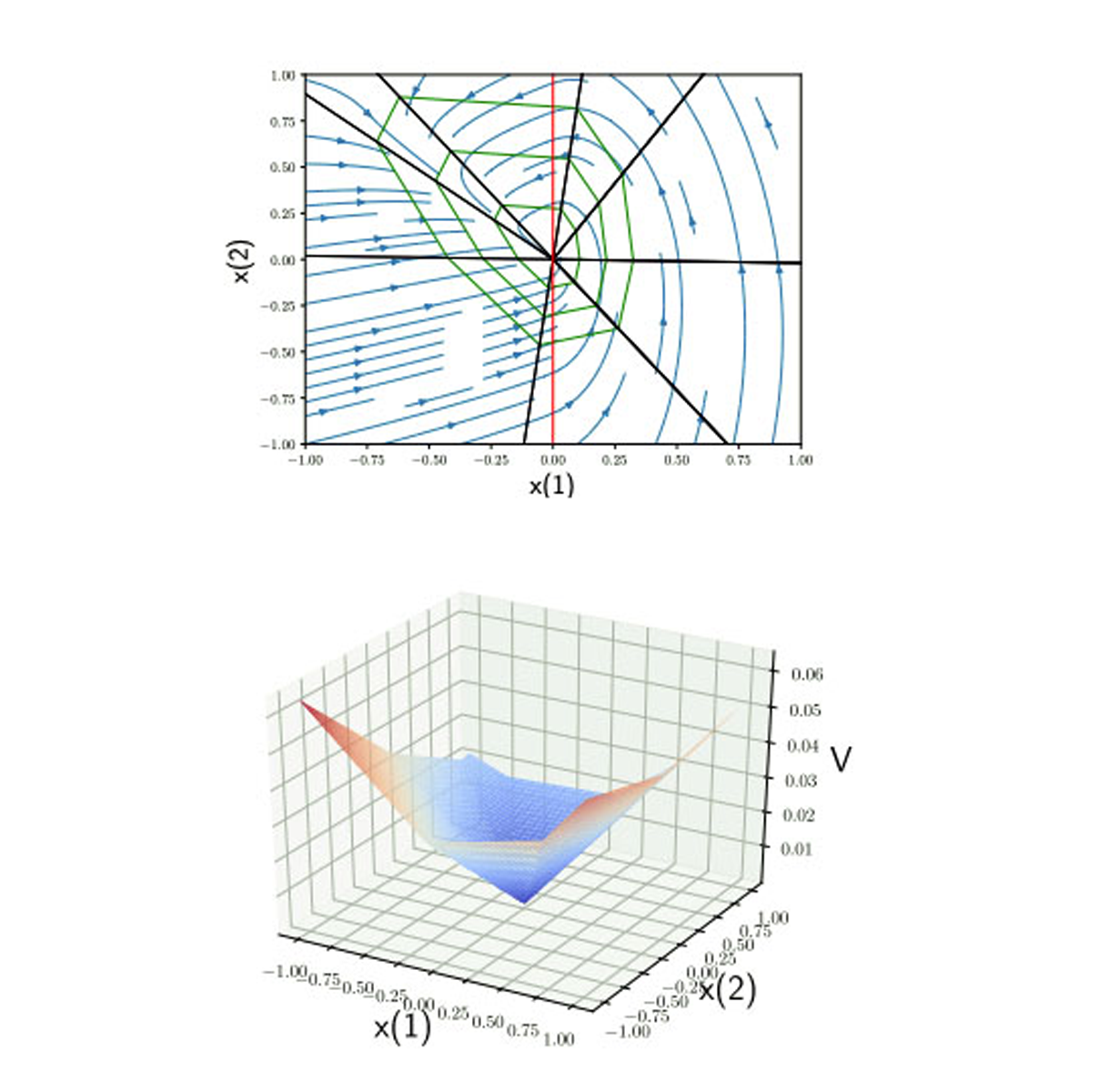
We introduce an algorithm for synthesizing and verifying piecewise linear Lyapunov functions to prove global exponential stability of piecewise linear dynamical systems. The Lyapunov functions we synthesize are parameterized by feedforward neural networks with leaky ReLU activation units. To train these neural networks, we design a loss function that measures the maximal violation of the Lyapunov conditions in the state space. We show that this maximal violation can be computed by solving a mixed-integer linear program (MILP). Compared to previous learning-based approaches, our learning approach is able to certify with high precision that the learned neural network satisfies the Lyapunov conditions not only for sampled states, but over the entire state space. Moreover, compared to previous optimization-based approaches that require a pre-specified partition of the state space when synthesizing piecewise Lyapunov functions, our method can automatically search for both the partition and the Lyapunov function simultaneously. We demonstrate our algorithm on both continuous and discrete-time systems, including some for which known strategies for partitioning of the Lyapunov function would require introducing higher order Lyapunov functions.


