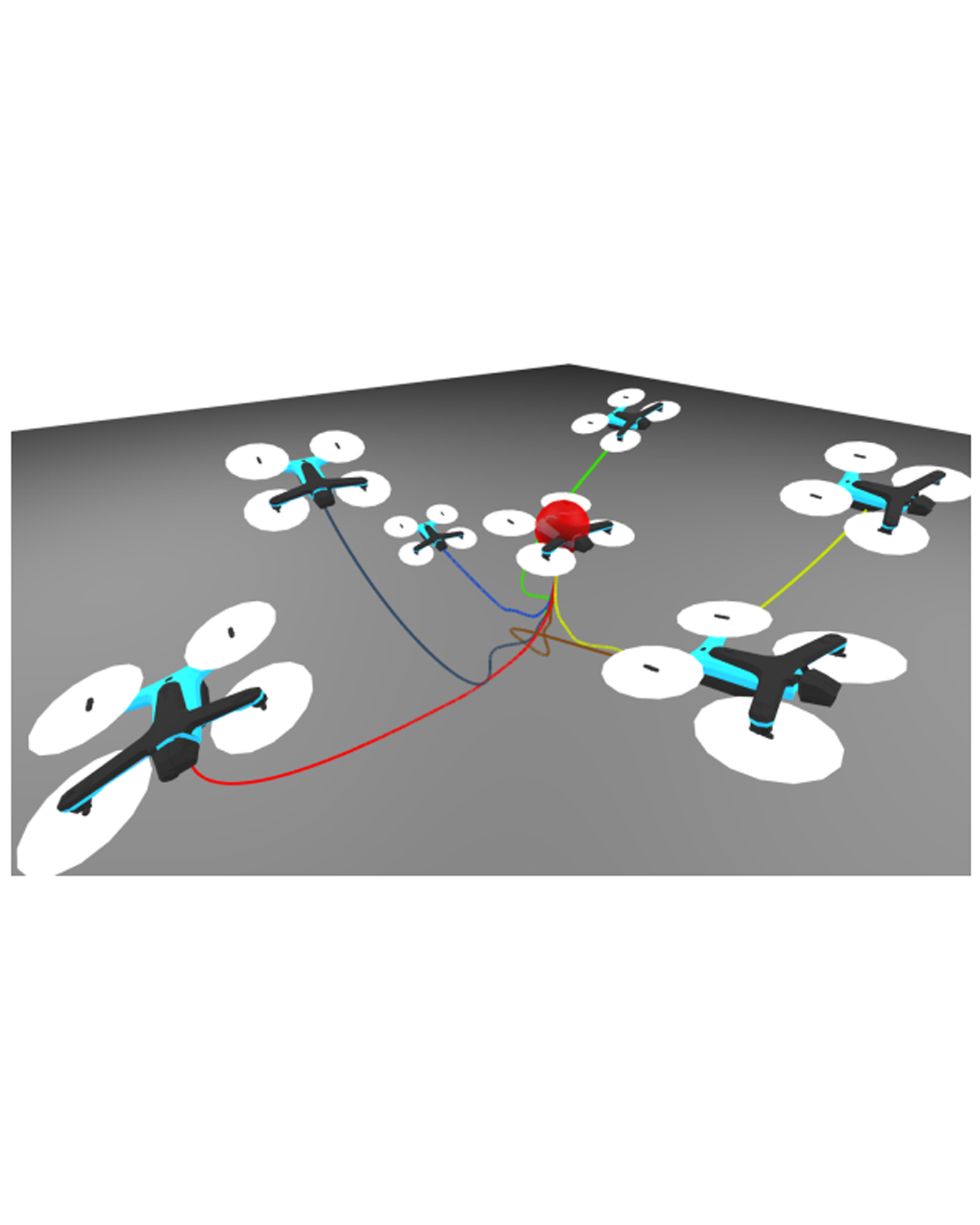
Safety and stability are essential properties of control systems. Control Barrier Functions (CBFs) and Control Lyapunov Functions (CLFs) are powerful tools to ensure safety and stability respectively. However, previous approaches typically verify and synthesize the CBFs and CLFs separately, satisfying their respective constraints, without proving that the CBFs and CLFs are compatible with each other, namely at every state, there exists control actions within the input limits that satisfy both the CBF and CLF constraints simultaneously. Ignoring the compatibility criteria might cause the CLF-CBFQP controller to fail at runtime. There exists some recent works that synthesized compatible CLF and CBF, but relying on nominal polynomial or rational controllers, which is just a sufficient but not necessary condition for compatibility. In this work, we investigate verification and synthesis of compatible CBF and CLF independent from any nominal controllers. We derive exact necessary and sufficient conditions for compatibility, and further formulate Sum-Of-Squares programs for the compatibility verification. Based on our verification framework, we also design a nominal-controller-free synthesis method, which can effectively expands the compatible region, in which the system is guaranteed to be both safe and stable. We evaluate our method on a non-linear toy problem, and also a 3D quadrotor to demonstrate its scalability. The code is open-sourced at https://github.com/hongkai-dai/compatible_clf_cbf. READ MORE