TRI Authors: Nikos Arechiga, Soonho Kong
All Authors: Sicun Gao, James Kapinski, Jyotirmoy Deshmukh, Nima Roohi, Armando Solar-Lezama, Nikos Arechiga, and Soonho Kong
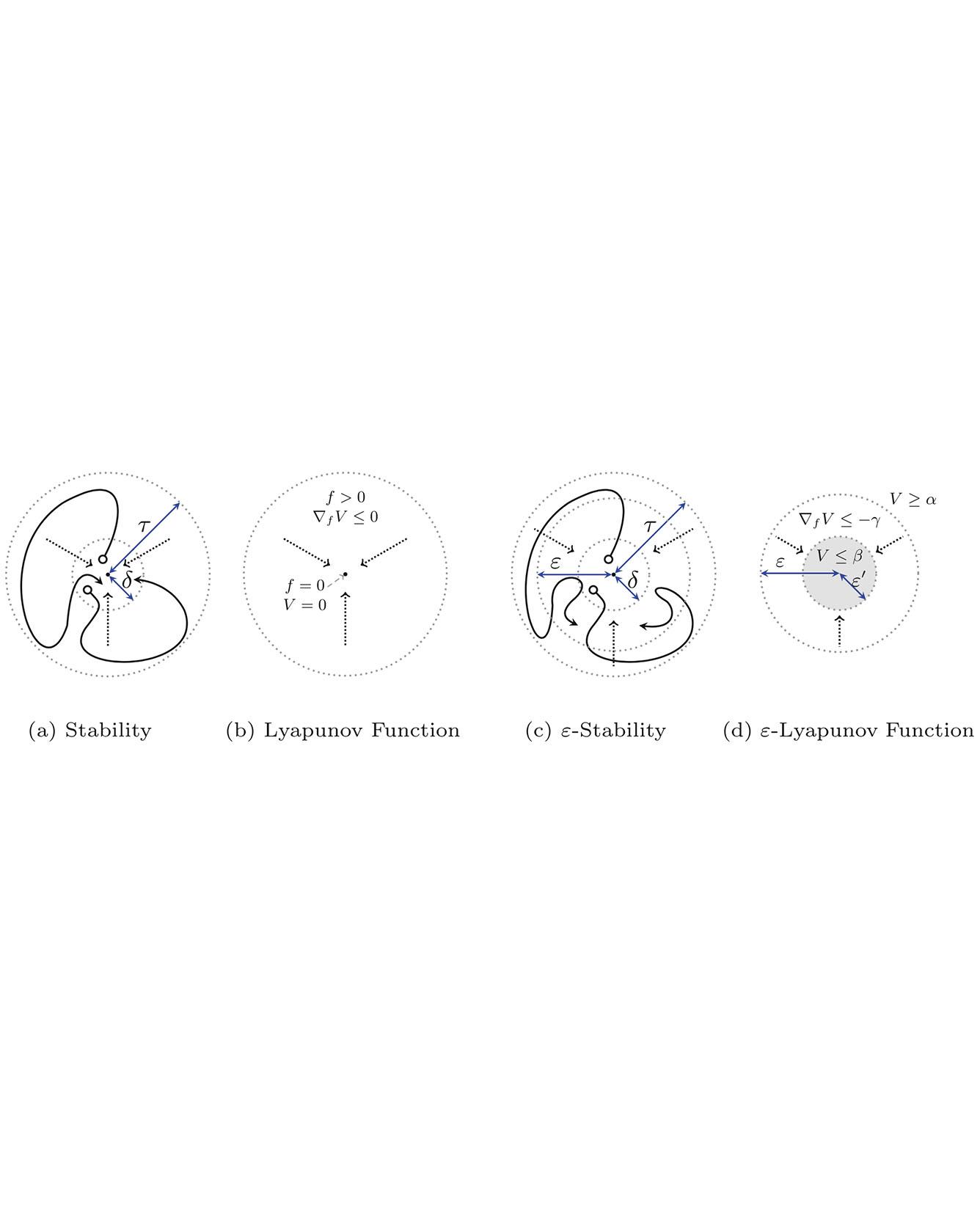
We formulate numerically-robust inductive proof rules for unbounded stability and safety properties of continuous dynamical systems. These induction rules robustify standard notions of Lyapunov functions and barrier certificates so that they can tolerate small numerical errors. In this way, numerically-driven decision procedures can establish a sound and relative-complete proof system for unbounded properties of very general nonlinear systems. We demonstrate the effectiveness of the proposed rules for rigorously verifying unbounded properties of various nonlinear systems, including a challenging powertrain control model. Read More
Citation: Gao, Sicun, James Kapinski, Jyotirmoy Deshmukh, Nima Roohi, Armando Solar-Lezama, Nikos Arechiga, and Soonho Kong. "Numerically-Robust Inductive Proof Rules for Continuous Dynamical Systems." In International Conference on Computer Aided Verification, pp. 137-154. Springer, Cham, 2019.


